Harris矩阵和Hessian矩阵

Harris 矩阵（使用的是一阶导数）

令 $ f(x,y) $ 表示图像，并令 $ f(x_{0},y_{0}) $ 表示以点 $ (x_{0},y_{0}) $ 为中心的一小块邻域图像（假设邻域图像的大小为 $ n $ × $ n $ ），将其移动一定量得到另一小块图像，则该两块图像的灰度差异（灰度变化）可以用如下表达式来衡量： \[ C(\Delta x,\Delta y) = \sum_{n\times n}w(x_{0},y_{0})[f(x_{0}+\Delta x,y_{0}+\Delta y) - f(x_{0},y_{0})]^2 \] 其中， $ w(x_{0},y_{0}) $ 是以点 $ (x_{0},y_{0}) $ 为中心的盒式加权函数或高斯加权函数

将图像 $ f(x,y) $ 在 $ x=x_{0},y=y_{0} $ 处进行泰勒展开，可得： \[ f(x_{0} + \Delta x,y_{0} + \Delta y) = f(x_{0},y_{0}) + \begin{pmatrix} f_{x}(x_{0},y_{0}) \\ f_{y}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} \\ + \frac{1}{2!}\begin{pmatrix} \Delta x & \Delta y\end{pmatrix} \begin{pmatrix} f_{xx}(x_{0},y_{0}) & f_{xy}(x_{0},y_{0} \\ f_{yx}(x_{0},y_{0}) & f_{yy}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} +o\lVert\Delta x^{2} + \Delta y^{2}\rVert \] 若只取线性展开项，则灰度差异（灰度变化）表达式变为： \[ C(\Delta x,\Delta y) = \sum_{n\times n}w(x_{0},y_{0})[\Delta xf_{x} (x_{0},y_{0}) + \Delta yf_{y}(x_{0},y_{0})]^2 \] 显然，平方项是一个实二次型，可使用矩阵表示法： \[ [\Delta xf_{x}(x_{0},y_{0}) + \Delta yf_{y}(x_{0},y_{0})]^2 = \begin{pmatrix} \Delta x & \Delta y\end{pmatrix} \begin{pmatrix} f^2_{x}(x_{0},y_{0}) & f_{x}f_{y}(x_{0},y_{0}) \\ f_{x}f_{y}(x_{0},y_{0}) & f^2_{y}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} \] 因加权求和运算是线性运算，故交换运算次序，得： \[ C(\Delta x,\Delta y) = \begin{pmatrix} \Delta x & \Delta y\end{pmatrix} \sum_{n\times n}w(x_{0},y_{0}) \begin{pmatrix} f^2_{x}(x_{0},y_{0}) & f_{x}f_{y}(x_{0},y_{0}) \\ f_{x}f_{y}(x_{0},y_{0}) & f^2_{y}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} \] 若令： \[ H = \sum_{n\times n}w(x_{0},y_{0}) \begin{pmatrix} f^2_{x}(x_{0},y_{0}) & f_{x}f_{y}(x_{0},y_{0}) \\ f_{x}f_{y}(x_{0},y_{0}) & f^2_{y}(x_{0},y_{0})\end{pmatrix} \] 则灰度差异（灰度变化）表达式变为：（这是一个实二次型） \[ C(\Delta x,\Delta y) = \begin{pmatrix} \Delta x & \Delta y\end{pmatrix} H \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} \]

因为 H 矩阵的主对角元（即两个平方项的系数）均大于零，因此上述实二次型在空间中是一个椭圆抛物面

为研究其变化率，此处便出现了两种思路：

• 研究其二阶导数（因为上述实二次型由一阶导数构成，一阶导数再求导数就是二阶导数），而其二阶导数就是 Hessian 矩阵
• 研究椭圆抛物面的水平切面（椭圆抛物面的切面都是椭圆，其中短轴方向是变化最快的方向，长轴方向是变化最慢的方向）

此处研究水平切面法，则不妨令上述实二次型的值为 1 ，有：

\[ \begin{pmatrix} \Delta x & \Delta y\end{pmatrix} H \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} = 1 \]

根据我前面写的文章：DIP 中的 Hessian 矩阵

可知矩阵 H 与上述椭圆存在关系：

矩阵的两个特征向量的方向分别对应着椭圆的长短轴的方向

矩阵的两个特征值分别对应着椭圆的半短轴、半长轴的平方的倒数

大特征值及其特征向量对应着椭圆的短轴，小特征值及其特征向量对应着椭圆的长轴

\[ \lambda_{min} = \frac{1}{a^2},\;\;\lambda_{max} = \frac{1}{b^2}\;\;(a是半长轴，b是半短轴，即a\geq b) \]

因此，我们说：大特征值对应的特征向量的方向代表着变化最慢的方向（灰度变化最小的方向），小特征值对应的特征向量的方向代表着变化最快的方向（灰度变化最大的方向）

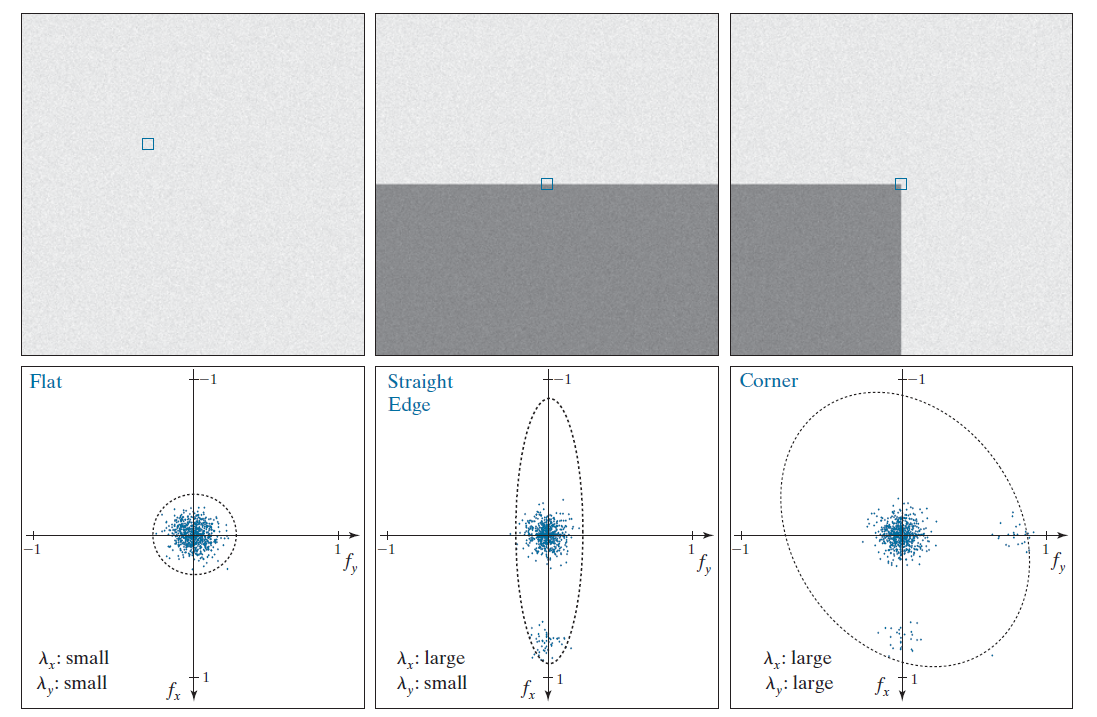
在图像中，存在“平坦区域”、“边缘”和“角”三种基本的特征（以下的长短轴代表的是 a 和 b ，不是特征值）

• 在“平坦区域”移动小块邻域图像，沿任何方向灰度变化都很小，即对应着两个小特征值（长轴），椭圆像一个很大的圆
• 在“边缘”移动小块邻域图像，沿着“边缘”移动的灰度变化很小，垂直“边缘”移动的灰度变化很大，即沿“边缘”对应着小特征值（长轴），而垂直“边缘”对应着大特征值（短轴），椭圆像一个很扁平很狭长的椭圆
• 在“角”移动小块邻域图像，沿任何方向灰度变化都很大，即对应着两个大特征值（短轴），椭圆像一个很小的圆

见下图：（注意，图中的长短轴表示的是特征值，不是 a 和 b （跟上面的描述恰好相反，注意区别）！（特征值大，变化大，特征值小，变化小））

因此，我们可以总结：

• 大特征值及其特征向量分别对应着椭圆的半短轴的平方的倒数和短轴的方向
• 小特征值及其特征向量分别对应着椭圆的半长轴的平方的倒数和长轴的方向
• 短轴方向变化快，大特征值方向变化快
• 长轴方向变化慢，小特征值方向变化慢

---

Hessian 矩阵（使用的是二阶导数）

上面提到过两种思路，一种是水平切面法（使用 Harris 矩阵分析），另一种是一阶导数再求导的变化率法（使用 Hessian 矩阵分析）

Hesssian 矩阵反映的是图像中局部曲率的变化，是梯度的变化率。在二元函数的泰勒展开中，Hesssian 矩阵天然地对应着椭圆，其特征值、特征向量与椭圆长短轴、长短轴方向之间的对应关系与上述 Harris 矩阵的分析是完全一致的

---

解释一些问题

• 为什么 Harris 矩阵使用的是一阶导数， Hessian 矩阵使用的是二阶导数，二者均能使用实二次型（对应椭圆）的分析方法呢？

因为 Harris 矩阵的构造很巧妙，它定义了一个灰度变化值 C ，该值的计算表达式可化为实二次型的形式

而 Hessian 矩阵完全基于泰勒展开，并没有人为地定义一个类似于 C 的度量，它直接反应梯度的变化率

二者有相似之处，但绝不是一个东西，应当加以区分

即 Harris 特征点检测与 Hessian 特征点检测是完全不同的两种方法

---

附上 Harris 特征点检测的代码

myHarris 函数：

function [x,y] = myHarris(img,n)
fx = imfilter(img,[-0.5;0;0.5],'symmetric');
fy = imfilter(img,[-0.5,0,0.5],'symmetric');
h = fspecial('gaussian',7,1);
fx2 = imfilter(fx.^2,h);
fy2 = imfilter(fy.^2,h);
fxy = imfilter(fx.*fy,h);
[rows,cols] = size(img);
H = cell(rows,cols);
R = zeros(rows,cols);
for i = 1:numel(img)
   H{i} = [fx2(i),fxy(i);fxy(i),fy2(i)];
   R(i) = det(H{i}) - 0.04*(trace(H{i}))^2;
end
w = 3;    % 半窗宽
label = zeros(rows,cols);
for i = 1+w:rows-w    % 在7×7邻域内进行非极大值抑制
    for j = 1+w:cols-w
        if R(i,j) == max(max(R(i-w:i+w,j-w:j+w))) ...
                && R(i,j) > 0.01*abs(max(R(:)))
            label(i,j) = 1;
        end
    end
end
[~,ind] = maxk(label(:).*R(:),n);    % 找出前n个响应最强的点
[x,y] = ind2sub([rows,cols],ind);
end

调用 demo ：

close all; clear; clc;
img = imread('house.tif');
if size(img,3) == 3
    img = rgb2gray(img);
end
img = double(img);
[x,y] = myHarris(img,100);
figure; imshow(img,[]);hold on;
plot(y,x,'r+','MarkerSize',8);
% 与自带函数对比
corners = detectHarrisFeatures(img);
figure; imshow(img,[]); hold on;
plot(corners.selectStrongest(100));

---

再附上 Hessian 特征点检测的代码

Hessian 特征点检测是依靠 Hessian 矩阵的行列式来进行判断的

注意，若行列式的值小于零，则表示 Hessian 矩阵是不定的（不满足各阶顺序主子式及各偶数阶顺序主子式大于零的正负定判断条件），此时该点不是极值点（即不是我们想要的特征点）

因此 Hessian 特征点检测又称为 DoH 检测（我们认为 DoH 是一个类似于 LoG 和 DoG 的算子）

myDoH 函数：

function [x,y] = myDoH(img,n)
fxx = imfilter(img,[1;-2;1],'replicate');
fyy = imfilter(img,[1,-2,1],'replicate');
fxy = imfilter(img,[1;0;-1]*[1,0,-1]/4,'replicate');
[rows,cols] = size(img);
H = cell(rows,cols);
R = zeros(rows,cols);
for i = 1:numel(img)
   H{i} = [fxx(i),fxy(i);fxy(i),fyy(i)];
   R(i) = det(H{i});    % 计算DoH
end
w = 3;    % 半窗宽
label = zeros(rows,cols);
for i = 1+w:rows-w    % 在7×7邻域内进行非极大值抑制
    for j = 1+w:cols-w
        if R(i,j) == max(max(R(i-w:i+w,j-w:j+w))) ...
                && R(i,j) > 0.01*abs(max(R(:)))
            label(i,j) = 1;
        end
    end
end
[~,ind] = maxk(label(:).*R(:),n);    % 找出前n个响应最强的点
[x,y] = ind2sub([rows,cols],ind);
end

调用 demo ：

close all; clear; clc;
img = imread('house.tif');
if size(img,3) == 3
    img = rgb2gray(img);
end
img = double(img);
[x,y] = myDoH(img,100);
figure; imshow(img,[]);hold on;
plot(y,x,'r+','MarkerSize',8);

仔细比较，体会二者的区别！

---

快速 DoH 算法

该算法用在 SURF 中，使用了盒式模板代替高斯二阶偏导模板，因为盒式模板与图像卷积可借助于积分图像进行快速运算