从泰勒展开说起
将一个一元函数 $ f(x) $ 在 $ x=x_{0} $ 处进行泰勒展开,可得: \[ f(x_{0} + \Delta x) = f(x_{0}) + f^{'}(x_{0})\Delta x + \frac{f^{''}(x_{0})}{2!}\Delta x^{2} + o\lVert\Delta x^{2}\rVert \] 同理,将一个二元函数(图像) $ f(x,y) $ 在 $ x=x_{0},y=y_{0} $ 处进行泰勒展开,可得: \[ f(x_{0} + \Delta x,y_{0} + \Delta y) = f(x_{0},y_{0}) + (f_{x}(x_{0},y_{0})\Delta x + f_{y}(x_{0},y_{0})\Delta y) + \\ \frac{1}{2!}(f_{xx}(x_{0},y_{0})\Delta x^{2} + 2f_{xy}(x_{0},y_{0})\Delta x\Delta y + f_{yy}(x_{0},y_{0})\Delta y^{2}) + o\lVert\Delta x^{2} + \Delta y^{2}\rVert \] 其中,我们假设混合二阶偏导数是相等的,即: \[ f_{xy}(x_{0},y_{0}) = f_{yx}(x_{0},y_{0}) \] 将其改写成矩阵相乘的形式,有: \[ f(x_{0} + \Delta x,y_{0} + \Delta y) = f(x_{0},y_{0}) + \begin{pmatrix} f_{x}(x_{0},y_{0}) \\ f_{y}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} \\ + \frac{1}{2!}\begin{pmatrix} \Delta x & \Delta y\end{pmatrix} \begin{pmatrix} f_{xx}(x_{0},y_{0}) & f_{xy}(x_{0},y_{0} \\ f_{yx}(x_{0},y_{0}) & f_{yy}(x_{0},y_{0})\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix} +o\lVert\Delta x^{2} + \Delta y^{2}\rVert \] 使用“对应”的思想去理解,应有: \[ \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix}\;\; 相当于 \;\;\Delta x \]
\[ \begin{pmatrix} \Delta x & \Delta y\end{pmatrix} \begin{pmatrix} \Delta x \\ \Delta y\end{pmatrix}\;\; 相当于 \;\;\Delta x^{2} \]
\[ \begin{pmatrix} f_{x}(x_{0},y_{0}) \\ f_{y}(x_{0},y_{0})\end{pmatrix}\;\; 相当于 \;\;f^{'}(x_{0}) \]
\[ \begin{pmatrix} f_{xx}(x_{0},y_{0}) & f_{xy}(x_{0},y_{0} \\ f_{yx}(x_{0},y_{0}) & f_{yy}(x_{0},y_{0})\end{pmatrix}\;\; 相当于 \;\;f^{''}(x_{0}) \]
即一元函数中的 标量变量 对应二元函数中的
两元素向量变量 ,一元函数中的 一阶导数斜率
对应二元函数中的 一阶导数梯度 ,一元函数中的
二阶导数斜率变化率 对应二元函数中的
二阶导数Hessian矩阵(梯度变化率)
,它是一种局部曲率(曲折度)的体现
总之,我们应记住这样一个结论(不严格去纠结):
Hessian矩阵就是二阶导数而二阶导数在判定函数极值中的重要性是不言而喻的
极值判定准则
- 一元函数情形
当一元函数 $ f(x) $ 在点 $ x=x_{0} $ 处的一阶导数 $ f^{'}(x_{0})=0 $ 时:
- 若二阶导数 $ f^{''}(x_{0})>0 $ ,则该点为
极小值点 - 若二阶导数 $ f^{''}(x_{0})<0 $ ,则该点为
极大值点 - 若二阶导数 $ f^{''}(x_{0})=0 $ ,则该点
无法判断
- 二元函数情形
当二元函数 $ f(x,y) $ 在点 $ (x_{0},y_{0}) $ 处的一阶导数(即梯度向量)为零时:
- 若
Hessian矩阵正定,即二阶导数值大于零,则该点为极小值点 - 若
Hessian矩阵负定,即二阶导数值小于零,则该点为极大值点 - 若
Hessian矩阵半正定或半负定(其它特征值都为正或负,但是至少有一个特征值为零),则该点无法判断 - 若至少有一个特征值大于零,且至少有一个特征值小于零,那么在大于零的特征值所对应的截面上有极小值,在小于零的特征值所对应的截面上有极大值,实际的二维曲面可以联想
马鞍面,该特殊点即为鞍点(该点不是极值点)
- 二维
Hessian矩阵正定性的判定
- 正定:两阶顺序主子式都大于零,即要求
两个特征值都大于零 - 负定:一阶顺序主子式小于零,二阶顺序主子式大于零,即要求
两个特征值都小于零 - 半正定:一个或两个特征值为零,可以检查该函数是否为常值函数或该函数在某一个维度上是否为常值
- 鞍点:一个特征值大于零,另一个特征值小于零(该点不是极值点)
二维 Hessian
矩阵和椭圆
一般形式的二元二次方程是双曲线方程,即: \[
a_{11}x^{2} + a_{22}y^{2} + (a_{12}+a_{21})xy = 1
\] 写成矩阵的形式为: \[
\begin{pmatrix}x & y\end{pmatrix}\begin{pmatrix} a_{11} & a_{12}
\\ a_{21} & a_{22}\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix} =
1
\] 当 $ a_{11},a_{22} $
同号时,该方程就变为一个椭圆方程,而且,椭圆的大小、形状、方位全由
实对称矩阵 决定
也就是说,该 实对称矩阵
的特征值和特征向量与椭圆的大小、形状、方位有着密切的关系
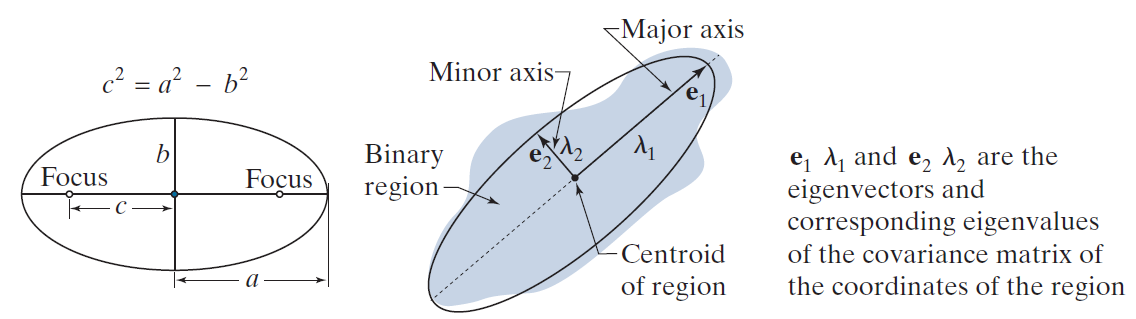
事实上,矩阵的两个特征向量的方向分别对应着椭圆的长短轴的方向
而矩阵的两个特征值分别对应着椭圆的半短轴、半长轴的平方的倒数
大特征值及其特征向量对应着椭圆的短轴,小特征值及其特征向量对应着椭圆的长轴(因为存在倒数关系)
具体可参看下图理解:
和图像的联系
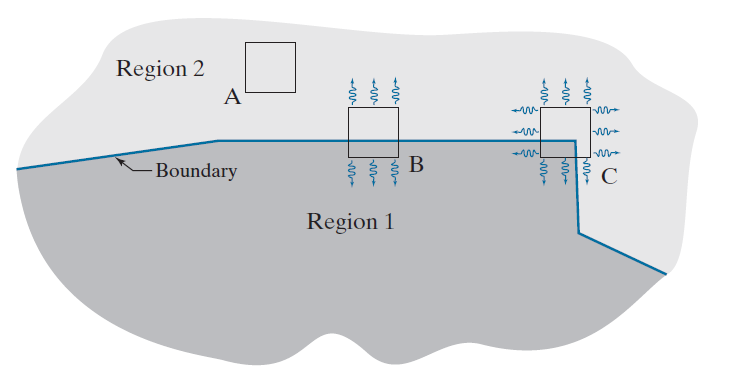
Hessian
矩阵可以量化图像中的“平坦区域”、“边缘”和“角”之间的差异,它体现了梯度的局部变化率(即梯度变化的快慢,又称局部曲率、局部曲折度),见下图:
某点的 Hessian
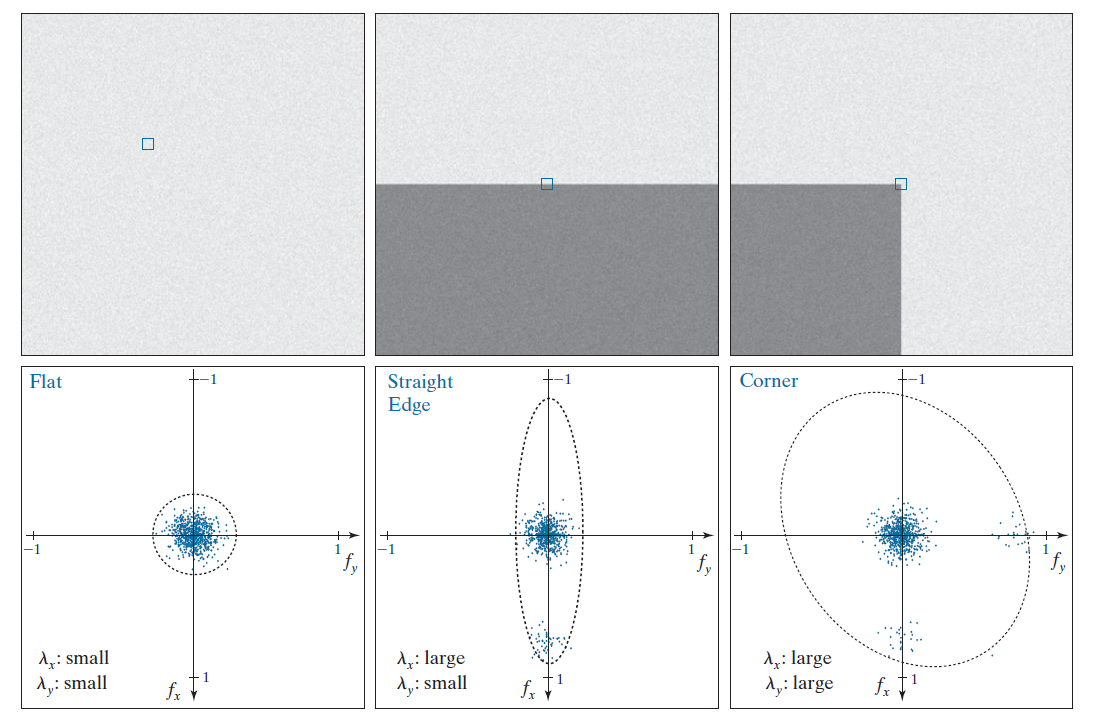
矩阵的特征值及特征向量可以很好地帮助我们判断图像的特征:
- 若两个特征值同号且值都较大,那么该点很有可能是斑点或者角点
- 都大于零,则为黑斑点或黑角点
- 都小于零,则为亮斑点或亮角点
- 若两个特征值同号且值都较小,那么该点很有可能位于平坦区域
- 若两个特征值同号且一个值较大一个值较小,那么该点很有可能位于边缘,且大特征值对应于垂直边缘的特征向量
详见以下图解:
图像中 Hessian
矩阵的计算
对于一幅图像 $ f(x,y) $ ,其 Hessian 矩阵可以表示为:
\[
\begin{pmatrix} \frac{\partial^{2} f}{\partial x^{2}} &
\frac{\partial^{2} f}{\partial x \partial y} \\ \frac{\partial^{2}
f}{\partial y \partial x} & \frac{\partial^{2} f}{\partial
x^{2}})\end{pmatrix}
\] 其中:(一阶导数都是按中心差分计算的) \[
\frac{\partial^{2} f}{\partial x^{2}} = f(x+1,y) + f(x-1,y) -2f(x,y)
\]
\[ \frac{\partial^{2} f}{\partial y^{2}} = f(x,y+1) + f(x,y-1) -2f(x,y) \]
\[ \frac{\partial^{2} f}{\partial x \partial y} = \frac{\partial^{2} f}{\partial y \partial x} = \frac{[f(x-1,y-1) + f(x+1,y+1)] - [f(x-1,y+1) + f(x+1,y-1)]}{4} \]