Hough线变换

一、 $ Hough $ 变换的参数平面（ $ Hough $ 平面）

在图像平面（ $ Image Plan $ ）的坐标系 $ xOy $ 中，直线方程的斜截式为： $ y = px + q $ ，其中 $ p $ 为斜率， $ q $ 为截距

假设上式所代表的某条（ $ p q $ 任意 ）直线上存在一点 $ (x_{i},y_{i}) $ ，则此点满足 $ y_{i} = px_{i} + q $ ，若将其改写，可变为 \[ q = -x_{i}p + y_{i} \] 试想，此时若构造一个 $ pOq $ 坐标系，则 $ -x_{i} $ 为斜率， $ y_{i} $ 为截距，这是一条确定的直线！

换言之， $ Hough $ 变换就是将图像平面的点映射为参数平面（ $ Parametric Plan $ ） 的线！

可以结合下图形象地理解：

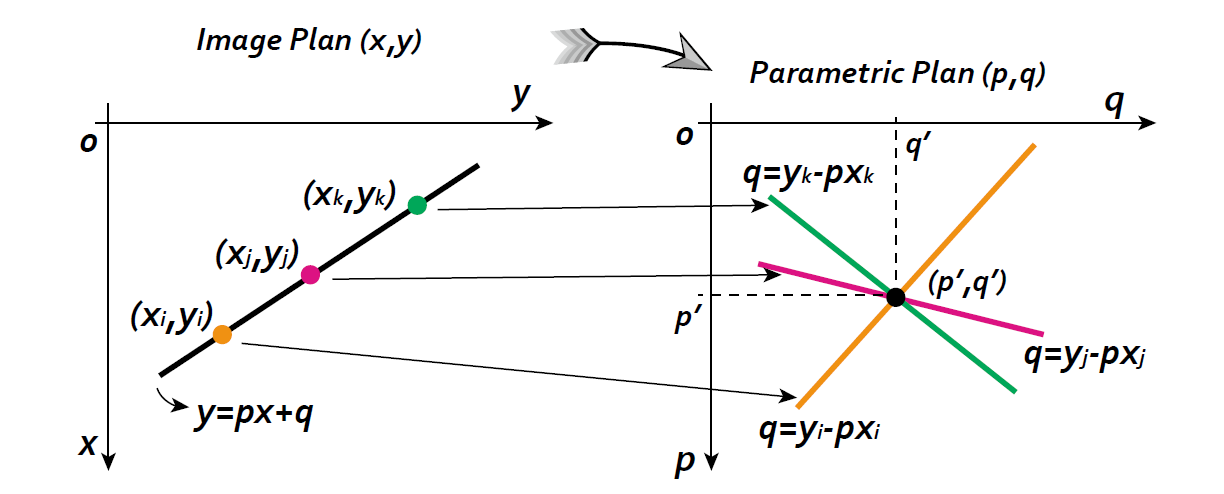
此时，可以在图像空间中考虑另一个点 $ (x_{j},y_{j}) $ ，它与点 $ (x_{i},y_{i}) $ 共同确定一条直线 $ q_{0} = -p_{0}x + y $

因为这两点具有同样的 $ p $ （斜率）和 $ q $ （截距），因此，二者在参数平面所代表的直线相交于同一点 $ (p_{0}, q_{0}) $

类似地，点 $ (x_{k},y_{k}) $ 所对应的直线也将经过点 $ (p_{0},q_{0}) $ ！

由此得出一个直观的结论：

图像平面中，同一条直线上的点在参数平面中所对应的线相交于一点

并且这一点的坐标为（图像平面直线的斜率，图像平面直线的截距）

---

二、在 $ Hough $ 平面中使用 $ voting $ 策略寻找直线

在参数平面中，越多的直线相交于同一点 $ (p_{0},q_{0}) $ ，那么在图像平面中就有越多的点位于直线 $ y = p_{0}x + q_{0} $ 上，也就是说

这条直线越像直线，这条直线比较明显，这条直线比较长，这条直线应该被认为是直线并且应该被标识出来

那么，问题来了，怎么样才能知道这个点 $ (p_{0},q_{0}) $ 被几条参数平面中的直线经过呢？ $ (p_{0},q_{0}) $ 又应该取什么值呢？

$ Hough $ 给出了一种遍历投票的解决办法，具体实现如下图所示：

（1）在 $ pOq $ 坐标系中划分网格（网格的精度根据实际要求自行确定），坐标轴的范围应从实际的最小斜率变化到

最大斜率、从实际的最小截距变化到最大截距（ $ p_{min} $ 到 $ p_{max} $ ， $ q_{min} $ 到 $ q_{max} $ ）

（2）对于图像平面中的点 $ (x_{i},y_{i}) $ ，遍历 $ p $ （ $ q $ 也行）的所有网格取值，代入表达式 $ q = -x_{i}p + y_{i}$ 中可得到

相应的 $ q $ （ $ p $ ）值，该值落在哪一个小网格内，就为该网格投一票

（3）遍历图像平面中所有的前景点，进行第（2）步操作，最终得到 $ pOq $ 坐标系中所有网格的投票情况

（4）筛选投票数较多（大于设定阈值）的网格，该网格所代表的 $ p $ 和 $ q$ 值便在图像平面中确定了直线 $ y_{i} = px_{i} + q $​

---

三、方法的特点以及局限性

方法的特点：

如上右图所示，网格划分得越精细，容错率就越低，就越容易受噪声的影响，所找的直线数量就越多

相反，网格划分得越粗糙，容错率就越高，在一定程度上能克服噪声的影响，但所找的直线越不准确

因此，网格的划分精度往往取决于实际的需求，而且，挑选筛选直线的阈值也是一门技术活

方法的局限性：

当图像平面中的直线接近竖直时， $ p $ 的值将变得特别大或特别小，即 $ |p| $ 趋于无穷时， $ pOq $ 平面将无法划分！

即使硬着头皮划分，计算机也会因庞大的计算量而内存溢出！

因此，传统意义上的 $ Hough $ 线变换无法寻找竖直直线！

---

四、解决传统的 $ Hough $ 线变换无法寻找竖直直线的问题

使用极坐标方程代替直角坐标方程即可完美地解决这个问题！首先观察下图 $ a) $ ：

在图像平面中，过原点做一条与直线垂直的垂线，该垂线的所代表的方向向量可写为： \[ (\ \rho cos(\theta),\ \rho sin(\theta)\ ) \] 设直线的方向向量为 $ (m,n) $ ，且经过点 $ (x_{i},y_{i}) $ ，则其方程可写为： \[ \frac{x-x_{i}}{m} = \frac{y-y_{i}}{n} \] 又因直线与垂线垂直，因此二者的方向向量满足： \[ (\ \rho cos(\theta),\ \rho sin(\theta)\ ) (m,\ n) = m\rho cos(\theta) + n\rho sin(\theta) = 0 \] 即： \[ m\rho cos(\theta) = -n\rho sin(\theta) \\ \\ \frac{m}{n} = -\frac{\rho sin(\theta)}{\rho cos(\theta)} \] 故有： \[ \frac{x-x_{i}}{y-y_{i}} = \frac{m}{n} = -\frac{\rho sin(\theta)}{\rho cos(\theta)} \] 令： \[ x_{i} = \rho cos(\theta) \;\;\;\; y_{i} = \rho sin(\theta) \] 代入，并化简整理，可得： \[ \frac{x-\rho cos(\theta)}{y-\rho sin(\theta)} = -\frac{\rho sin(\theta)}{\rho cos(\theta)} \\ \\ \rho cos(\theta)x - \rho^2cos^2(\theta) = \rho^2sin^2(\theta) - \rho sin(\theta)y \\ \\ \rho cos(\theta)x + \rho sin(\theta)y = \rho^2cos^2(\theta) + \rho^2sin^2(\theta) = \rho^2 \\ \\ \rho = xcos(\theta) + ysin(\theta) \] 可以很明显地看出，在参数平面上，一个点映射成了一条正余弦曲线，并且横纵坐标轴的取值范围缩减为： \[ \rho \in [-D,D] \;\;\;\;\;\; \theta \in [-90^o,90^o] \] 其中 $ D $ 为图像平面中对角之间的最大距离

寻找直线的遍历投票思想在这里是一样的，只不过参数平面交点的获得由直线相交变为了正余弦曲线相交

---

五、一些 $ Hough $ 线变换的实例（建立直观感受）

六、 $ Hough $ 线变换的实现

函数 myHoughLine 实现了 $ Hough $ 线变换，代码如下：

function myHoughLine(I,lineNum)
%% 参数说明
% I为灰度图像
% lineNum为要提取的直线数量

%% Hough线变换
BW = edge(I,'canny');    % 提取边缘，以作为Hough线变换的前景
[row,col] = size(BW);
D = ceil(sqrt(row^2 + col^2));    % 图像平面的对角距离，为避免索引时超出数组边界，向上取整
Rho = -D:D; Theta = -90:90;    % 定义参数平面的取值范围
Scores = zeros(length(Rho),length(Theta));    % 创建voting矩阵
[x,y] = find(BW == 1);    % 取出前景像素作为voting点
rho = round(x.*cosd(Theta) + y.*sind(Theta));
for i = 1:size(rho,1)
    for j = 1:length(Theta)
        Scores(D + rho(i,j) + 1,j) = Scores(D + rho(i,j) + 1,j) + 1;    % 遍历投票
    end
end
lineMaxValue = maxk(Scores(:),lineNum);
[lineRho,lineTheta] = find(Scores >= lineMaxValue(lineNum),lineNum);
lineRho = lineRho - D - 1;    % 记得转换回来
lineTheta = lineTheta - 90 - 1;

%% 绘制“最强的”lineNum条直线
figure; imshow(I); hold on;
for k = 1:lineNum
   n = 0.05*row:0.95*row;
   m = (-cosd(lineTheta(k))*n + lineRho(k)) / sind(lineTheta(k));
   m(m < 0.05*col | m > 0.95*col) = NaN;    % 绘制范围不要超过图像边界
   plot(m,n,'c','Linewidth',2);
end
hold off;
end

测试代码如下：

close all;clear;clc;tic;
I = imread('airport.tif');
if size(I,3) == 3
    I = rgb2gray(I);
end
myHoughLine(I,3);toc;

对一张机场航拍图进行主干道提取：

这是原图（可以看出一共有3条主干道）

这是使用 $ Hough $ 线变换的提取结果图

七、附录： $ Hough $ 圆变换

$ Hough $ 圆变换的思想与线变换是一致的，区别仅在于参数空间的维数不同。（ $ Hough $ 圆变换的参数空间为 $ a,b,r $ 三维）